Home » matematika » BANGUN DATAR SEGITIGA SAMA KAKI, SAMA SISI, SEMBARANG

BANGUN DATAR SEGITIGA SAMA KAKI, SAMA SISI, SEMBARANG

BANGUN DATAR SEGITIGA SAMA KAKI, SAMA SISI, SEMBARANG

PENGERTIAN BANGUN DATAR

Bangun datar merupakan sebutan untuk bangun-bangun dua dimensi. yaitu bangun yang memiliki panjang dan lebar saja. panjang disimbolkan P dan lebar disimbolkan L

JENIS-JENIS BANGUN DATAR

Jenis bangun datar bermacam-macam, antara lain persegi, persegi panjang, segitiga, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran.
Nama-nama Bangun Datar
  • Persegi Panjang, yaitu bangun datar yang mempunyai sisi berhadapan yang sama panjang, dan memiliki empat buah titik sudut siku-siku.
  • Persegi, yaitu persegi panjang yang semua sisinya sama panjang.
  • Segitiga, yaitu bangun datar yang terbentuk oleh tiga buah titik yang tidak segaris.. macam macamnya: segitiga sama sisi, segitiga sama kaki, segitiga siku-siku, segitiga sembarang
  • Jajar Genjang, yaitu segi empat yang sisinya sepasang-sepasang sama panjang dan sejajar.
  • Trapesium, yaitu segi empat yang memiliki tepat sepasang sisi yang sejajar.
  • Layang-layang, yaitu segi empat yang salah satu diagonalnya memotong tegak lurus sumbu diagonal lainnya.
  • Belah Ketupat, yaitu segi empat yang semua sisinya sama panjang dan kedua diagonalnya saling berpotongan tegak lurus.
  • Lingkaran, yaitu bangun datar yang terbentuk dari himpunan semua titik persekitaran yang mengelilingi suatu titik asal dengan jarak yang sama. jarak tersebut biasanya dinamakan r, atau radius, atau jari-jari.

RUMUS RUMUS BANGUN DATAR

Rumus Bangun Datar
  • Rumus Persegi
Luas = s x s = s2 ( Luas = ½ x diagonal (d) 1 x diagonal (d) 2, 'sudah dibuktikan' )
Keliling = 4 x s
dengan s = panjang sisi persegi
  • Rumus Persegi Panjang
Luas = p x l
p = Luas : lebar
l = Luas : panjang
Keliling = 2p + 2l = 2 x (p + l)
dengan p = panjang persegi panjang, dan l = lebar persegi panjang
  • Rumus Segitiga
Luas = ½ x a x t
dengan a = panjang alas segitiga, dan t = tinggi segitiga
Panjang sisi miring segitiga siku-siku dicari dengan rumus Phytagoras (A2 + B2 = C2)
  • Rumus Jajar Genjang
Luas = a x t
dengan a = panjang alas jajargenjang, dan t = tinggi jajargenjang
  • Rumus Trapesium
Luas = ½ x (s1 + s2) x t
dengan s1 dan s2 = sisi-sisi sejajar pada trapesium, dan t = tinggi trapesium
  • Rumus Layang-layang
Luas = ½ x diagonal (d) 1 x diagonal (d) 2
  • Rumus Belah Ketupat
Luas = ½ x diagonal (d) 1 x diagonal (d) 2
  • Rumus Lingkaran
Luas = π (pi) x jari-jari (r) 2
        = πr2

BANGUN DATAR SEGITIGA, Sifat Sifat Dan Rumus Segitiga

Pada bangun datar Segitiga, mempunyai sifat-sifat diantaranya :
  • Mempunyai 3 sisi dan 3 titik sudut
  • Jumlah ketiga sudutnya 180 derajat
  • Luas = ½ x a x t
  • Keliling = AB + BC + AC 

Bangun segitiga terdiri dari 4 macam, jika dibedakan menurut panjang susu segitiga tersebut yaitu : segitiga sama sisi, segitiga sama kaki, segitiga siku-siku dan segitiga sembarang.

Pada bangun datar Segitiga sama sisi, mempunyai sifat-sifat diantaranya :
Sifat Sifat Bangun Datar - Rumus Bangun Datar
  • Mempunyai 3 buah sisi sama panjang, yaitu AB=BC=CA
  • Mempunyai 3 buah sudut yang besar , yaitu <ABC , <BCA, <CAB
  • Mempunyai 3 sumbu simetri.
  • Mempunyai 3 simetri putar dan 3 simetri lipat

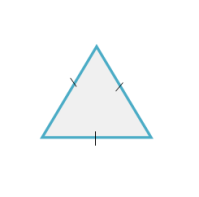
Pada bangun datar Segitiga sama kaki, mempunyai sifat-sifat diantaranya :
Sifat Sifat Bangun Datar - Rumus Bangun Datar
  • Mempunyai 2 buah sisi yang sama panjang, yaitu BC=AC
  • Mempunyai 2 buah sudut sama besar, yaitu < BAC = <ABC
  • Mempunyai 1 sumbu simetri.
  • Dapat menempati bingkainya dalam dua cara.
Pada bangun datar Segitiga siku-siku, mempunyai sifat-sifat diantaranya :
Sifat Sifat Bangun Datar - Rumus Bangun Datar
  • Mempunyai 1 buah sudut siku-siku,yaitu <BAC
  • Mempunyai 2 buah sisi yang saling tegak lurus, yaitu BA dan AC
  • Mempunyai 1 buah sisi miring yaitu BC
  • Sisi miring selalu terdapat di depan sudut siku-siku.
  • Segitiga siku-siku samakaki memiliki 1 sumbu simetri.

Pada bangun datar Segitiga sembarang, mempunyai sifat-sifat diantaranya :
Sifat Sifat Bangun Datar - Rumus Bangun Datar
  • Mempunyai 3 buah sisi yang tidak sama panjang.
  • Mempunyai 3 buah sudut yang tidak sama besar.


Pengertian Bangun Datar segitiga

A. Pengertian segitiga
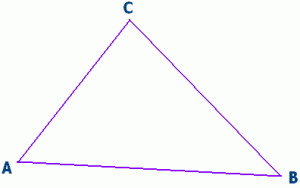c1            Perhatikan sisi-sisinya, ada berapa sisi-sisi yang membentuk segitiga ABC? Sisi-sisi yang membentuk segitiga ABC berturut-turut
            adalah AB, BC, dan AC. Sudut-sudut yang terdapat pada segitiga ABC sebagai berikut.
               a. sudut A atau sudut BAC atau sudut CAB.
               b. sudut B atau sudut ABC atau sudut CBA.
               c. sudut C atau sudut ACB atau sudut BCA.
            Jadi, ada tiga sudut yang terdapat pada Δ ABC.
Dari uraian di atas dapat disimpulkan sebagai berikut :
 Segitiga adalah bangun datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga buah titik  sudut.
B. Jenis-jenis Segitiga
Jenis-jenis suatu segitiga dapat ditinjau berdasarkan :
a. Panjang sisi-sisinya
           1. Segitiga sebarang Segitiga sebarang adalah segitiga yang sisi-sisinya tidak sama panjang. Pada gambar dibawah ini  merupakan
                segitiga sembarang dimana AB tidak sama dengan BC Tidak sama dengan AC
sembaran
          2. Segitiga sama kaki
Segitiga sama kaki adalah segitiga yang mempunyai dua buah sisi sama panjang. Pada gambar dibawah ini merupakan segitiga
               sama kaki ABC dengan AB = BC.
images
          3. Segitiga sama sisi
                Segitiga sama sisi adalah segitiga yang memiliki tiga buah sisi sama panjang dan tiga buah sudut sama besar. Segitiga  pada
                Gambar dibawah ini merupakan segitiga sama sisi.
segitiga sama sisi
b. Besar sudut-sudutnya
1. Segitiga lancip
           Segitiga lancip adalah segitiga yang ketiga sudutnya merupakan sudut lancip, sehingga sudut-sudut yang terdapat pada
          segitiga tersebut besarnya antara 0 derajat  dan 90 derajat . Pada Gambar dibawah ini, ketiga sudut pada Δ ABC adalah sudut      
          lancip.
     2. Segitiga tumpul
         Segitiga tumpul adalah segitiga yang salah satu sudutnya merupakan sudut tumpul. Pada  Δ ABC di samping, sudut  ABC adalah
         sudut tumpul.
g
images (3)     3. Segitiga siku-siku
          Segitiga siku-siku adalah segitiga yang salah satu sudutnya merupakan sudut siku-siku (besarnya 90o). Pada Gambar di bawah
          ini, Δ ABC siku-siku di titik C.

c. Panjang sisi dan besar sudutnya.
images (4)1.  Segitiga siku-siku sama kaki         
           Segitiga siku-siku sama kaki adalah segitiga yang kedua sisinya sama panjang dan salah satu sudutnya merupakan sudut siku-
           siku (90 derajat).
           Pada Gambar di bawah ini, Δ abc siku-siku di titik b, dengan ab = ac.
       

h9     2. Segitiga tumpul sama kaki
          Segitiga tumpul sama kaki adalah segitiga yang kedua sisinya sama panjang dan salah satu sudutnya merupakan sudut 
          tumpul.
          Sudut tumpul Δ PQR pada Gambar di bawah ini adalah sudut  P, dengan PR = PQ.
Categories:
Pin It

Related Post:



0 komentar :

Post a Comment

Silahkan Berkomentar Sesuai Dengan Topik, Jangan Menggunakan Kata-Kata Kasar, Komentar Dengan Link Aktif Tidak Akan Dipublikasikan

ttd

Admin Blog