Home » matematika » zona matematika cara cepat menghitung luas segitiga dengan Pascal

zona matematika cara cepat menghitung luas segitiga dengan Pascal



Menghitung Luas Segitiga


Alas :
Tinggi :

zona matematika cara cepat menghitung luas segitiga dengan blog

Temukan alas dan tinggi segitiga. Alas segitiga adalah panjang salah satu sisi yang biasanya berada di sisi bawah segitiga. Tinggi segitiga adalah panjang dari alas ke titik puncak segitiga yang tegak lurus dengan alas. Dalam segitiga siku-siku, panjang alas dan tingginya adalah dua sisi yang membentuk sudut 90 derajat. Akan tetapi, dalam segitiga bukan siku-siku, seperti di bawah ini, tingginya adalah tegak lurus titik tengah segitiga.
  • Setelah Anda menemukan alas dan tinggi segitiga, Anda bisa menggunakan rumusnya.
Masukkan nilai alas dan tinggi. Carilah nilai alas dan tinggi segitiga dan masukkan angkanya ke dalam persamaan. Dalam contoh ini, tinggi segitiga adalah 3 cm dan alasnya adalah 5 cm. Inilah rumus yang kita gunakan setelah memasukkan nilainya:
  • Luas = 1/2 x (3 cm x 5 cm)
Tuliskan rumus untuk mencari luas segitiga. Rumus untuk masalah seperti ini adalah Luas = 1/2(alas x tinggi), atau 1/2(at). Setelah Anda menuliskannya, Anda bisa memasukkan panjang tinggi dan alas.

Selesaikan persamaannya. Anda bisa mengalikan tinggi dengan alas terlebih dahulu karena angka-angka itu berada dalam tanda kurung, kemudian mengalikan hasilnya dengan 1/2. Tetapi, ketahuilah bahwa mengalikan ketiga angka ini dengan urutan apapun akan menghasilkan hasil yang sama. Ingatlah untuk menuliskan jawabanmu dalam satuan kuadrat karena Anda mengerjakan soal dua dimensi. Inilah jawaban akhirnya:
  • Luas = 1/2 x (3 cm x 5 cm)
  • Luas = 1/2 x 15 cm2
  • Luas = 7,5 cm2

Hitunglah setengah keliling segitiga. Untuk mencari setengah keliling segitiga, yang harus Anda lakukan adalah menambahkan semua sisinya dan membagi hasilnya dengan 2. Rumus untuk mencari setengah keliling segitiga adalah: setengah keliling = (panjang sisi a + panjang sisi b + panjang sisi c) / 2, atau s = (a + b + c) / 2. Karena Anda sudah mengetahui bahwa panjang ketiga sisi segitiga siku-sikunya adalah 3 cm, 4 cm, dan 5 cm, Anda bisa memasukkannya ke dalam persamaan dan mencari setengah kelilingnya:
  • s = (3 + 4 + 5)/2
  • s = 12/2
  • s = 6
Masukkan nilai yang sesuai ke dalam rumus untuk mencari luas segitiga.Rumus untuk mencari luas segitiga disebut teorema Heron, seperti berikut: Luas = √{s (s - a)(s - b)(s - c)}. Ingatlah dari langkah sebelumnya bahwa s adalah setengah keliling dan a, b, dan c adalah ketiga sisi segitiga. Menggunakan “urutan pengerjaan”, mulailah menyelesaikan semua yang ada di dalam tanda kurung, kemudian semua yang ada di dalam akar, dan akhirnya menyelesaikan akar kuadrat. Inilah rumus yang kita gunakan setelah memasukkan nilai yang sudah diketahui: [2]
  • Luas = √{6 (6 - 3)(6 - 4)(6 - 5)}
Kurangkan nilai dari tiga perhitungan di dalam tanda kurung. Untuk melakukannya, langsung kurangkan saja 6 – 3, 6 – 4, dan 6 – 5, seperti ini:
  • 6 - 3 = 3
  • 6 - 4 = 2
  • 6 - 5 = 1
  • Luas = √{6 (3)(2)(1)}
Kalikan hasil tiga perhitungan di dalam kurung. Kalikan saja 3 x 2 x 1 dan hasilnya 6. Anda harus mengalikan angka-angka ini dahulu sebelum mengalikannya dengan angka 6 karena berada di dalam tanda kurung.
Kalikan hasil perkalian sebelumnya dengan s. Sekarang, kalikan 6 dengan setengah keliling, yang juga bernilai 6. 6 x 6 = 36.


Temukan akar kuadratnya. 36 adalah kuadrat sempurna dan √36 = 6. Jangan lupa satuan awal yang Anda gunakan – centimeter. Tuliskan jawaban akhirmu dalam centimeter kuadrat. Luas segitiga dengan sisi 3, 4, dan 5 cm adalah 6 cm2.

Temukan sisi segitiga sama sisi. Sebuah segitiga sama sisi memiliki panjang sisi dan sudut yang sama. Anda akan mengetahui jika Anda menggunakan segitiga sama sisi karena Anda sudah diberitahu atau karena Anda mengetahui bahwa sudut atau panjang semua sisinya sama. Nilai salah satu sisi segitiga sama sisi ini adalah 6 cm. Tuliskan.
  • Jika Anda mengetahui bahwa Anda menggunakan segitiga sama sisi tetapi hanya mengetahui kelilingnya, bagilah kelilingnya dengan 3. Misalnya, panjang sisi segitiga sama sisi dengan keliling 9 adalah 9/3 yaitu 3.
Tuliskan rumus yang digunakan untuk menemukan luas segitiga sama sisi.Rumus untuk menyelesaikan masalah ini adalah luas = (s^2)(√3)/4. Perhatikan bahwa s adalah “sisi.”


Masukkan panjang sisinya ke dalam persamaan. Pertama, kuadratkan panjang sisinya, 6 menjadi 36. Kemudian, temukan nilai desimal dari √3, jika jawabanmu harus dalam bentuk desimal. Masukkan √3 ke dalam kalkulatormu untuk mendapatkan 1,732. Kemudian, bagilah angka ini dengan 4. Perhatikan bahwa Anda juga bisa membagi 36 dengan 4, kemudian mengalikannya dengan √3 – urutan pengerjaan tidak akan mempengaruhi jawaban.

Selesaikan. Sekarang, Anda hanya harus menyelesaikan matematikanya. 36 x √3/4 = 36 x 0,433 = 15,59 cm2. Luas segitiga sama sisi dengan panjang sisi 6 cm adalah 15,59 cm2.

Carilah panjang kedua sisi dan sudut antara kedua sisi. Sudut antara kedua sisi adalah sudut yang berada di antara dua sisi segitiga. Anda harus mengetahui nilai-nilai ini untuk mencari luas segitiga menggunakan cara ini. Misalkan Anda menggunakan segitiga dengan ukuran berikut:
  • sudut A = 123ยบ
  • sisi b = 150 cm
  • sisi c = 231 cm
Tuliskan rumus untuk menemukan luas segitiga. Rumus untuk mencari luas segitiga dengan dua sisi dan sudut di antara keduanya diketahui, adalah: Luas = 1/2(b)(c) x sinA. Dalam persamaan ini, "b" dan "c" menunjukkan panjang dua sisi dan "A" menunjukkan sudut. Anda harus selalu menggunakan sinus sudut dalam persamaan ini.

Masukkan nilai-nilainya ke dalam persamaan. Inilah persamaannya setelah nilainya dimasukkan:
  • Luas = 1/2(b)(c) x sinA
  • Luas = 1/2(150)(231) x sinA
Selesaikan. Untuk menyelesaikan persamaan ini, pertama, kalikan kedua sisi dan bagilah hasilnya dengan 2, kemudian kalikan hasilnya dengan sinus sudut. Anda bisa menemukan nilai sinus sudut dengan memasukkannya ke fungsi "sin" di kalkulatormu. Jangan lupa untuk menuliskan jawaban dalam satuan kuadrat. Inilah caranya:
  • Luas = 1/2(150)(231) x sinA
  • Luas = 1/2(34,650) x sinA
  • Luas = 17,325 x sinA
  • Luas = 17,325 x .8386705
  • Luas = 14,530 cm2

KELILING DAN LUAS SEGITIGA

Sebelum dibicarakan tentang Keliling dan Luas Segitiga, akan dibahas tentang alas dan tinggi (garis tinggi).

Garis Tinggi Segitiga

Garis tinggi adalah garis yang ditarik dari salah satu titik sudut dan tegak lurus dengan sisi di depannya.
Karena segitiga memiliki tiga buah titik sudut, maka setiap segitiga memiliki tiga buah garis tinggi.

Alas Segitiga

Setiap sisi segitiga dapat dipandang sebagai alas sebuah segitiga.
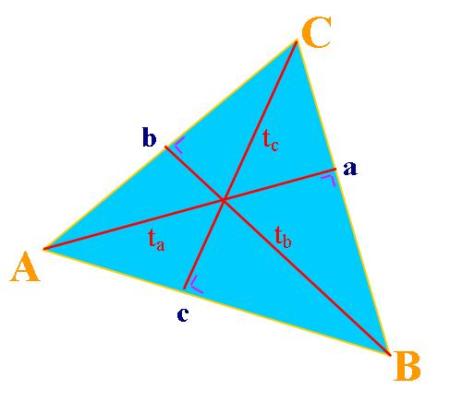
Perhatikan gambar berikut :
alas-tinggi
Sisi  AB disebut juga sebagai sisi c, karena letaknya di depan sudut C. Demikian juga sisi  BC dan  AC disebut juga sebagai sisi a dan sisi b
Garis tinggi yang dibuat dari titik sudut C disebut tc, karena tegak lurus dengan alas atau sisi c atau AB. Demikian pula dengan garis tinggi yang dibuat dati titik sudut B dan A disebut tb dan ta.

Keliling Segitiga

Keliling sebuah bidang datar adalah jumlah panjang sisi-sisi yang membatasi bidang datar tersebut. Jadi, keliling segitiga adalah jumlah panjang ketiga sisinya.
kell
Jika K menyatakan keliling segitiga ABC maka
K = AB + BC + AC
K = c + a + b
Jadi keliling segitiga dirumuskan sebagai berikut:
kell-rmus
Luas Segitiga

Luas segitiga adalah setengah hasil kali panjang alas dan tingginya
luas
Keterangan :
a = alas
b = tinggi

Rumus Mencari Luas Segitiga (Sama Sisi, Sama Kaki, Sembarang) dan Keliling Segitiga
Segitiga merupakan suatu bidang datar yang memiliki 3 sisi dan 3 titik sudut. Untuk mencari rumus luas segitiga itu bergantung dari setiap sisinya, ada yang sama sisi, sama kaki, dan sembarang.

Segitiga dapat dibagi menjadi tiga yaitu :
  1. Segitiga sama sisi, yaitu segitiga yang memiliki panjang sisi yang sama. Jika setiap sisinya sama maka otomatis sudutnya juga akan sama yaitu 60 derajat.
  2. Segitiga sembarang, yaitu segitiga yang pada ketiga sisinya memiliki ukuran yang berbeda, maka ketiga titik sudutnya juga berbeda.
  3. Segitiga sama kaki, yaitu segitiga yang memiliki dua sisi yang sama pada segitiga tersebut. Oleh karena itu akan ada dua titik sudut yang sama besar.
Sebelum kita membahas rumus luas segitiga,kita bahas dulu rumus keliling segitiga. Rumus keliling segitiga didapatkan dengan menjumlah setiap sisi pada segitiga tersebut, maka kita dapatkan rumus :

K = sisi1 + sisi2 + sisi3

Selanjutnya kita bahas masalah luas segitiga. Rumus umum luas segitiga yaitu :

L = 1/2 x a x t

Dimana a merupakan panjang alas segitiga dan t merupakan tinggi segitiga.

Rumus Luas Segitiga Sama Sisi

Segitiga sama sisi mempunyai rumus luas sebagai berikut :

Rumus Luas Segitiga Sama Sisi
Dimana a merupakan panjang sisi segitiga sama sisi tersebut.

Rumus Luas Segitiga Sembarang

Segitiga sembarang mempunyai rumus sebagai berikut :

Rumus Luas Segitiga Sembarang
Dimana s merupakan setengah dari keliling segitiga yaitu :
s = 1/2 (a + b + c)

Rumus Luas Segitiga Sama Kaki

Segitiga sama kaki mempunyai rumus sebagai berikut :

L = 2 x (1/2 x a x t)
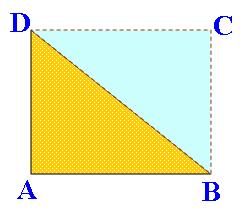
Pada segitiga sama kaki akan terdapat 2 segitiga siku-siku yang merupakan hasil pembagian garis tinggi segitiga sama kaki.

Dari gambar diatas kita dapat melihat bahwa DC merupakan garis tinggi yang membagi segitiga ABC menjadi ACD dan BCD. panjang AD dan DB sama dan panjang AC dan BC adalah sama. Maka rumus luas segitiga sama kaki juga dapat ditulis menjadi :

L = a x t

Segitiga merupakan sebuah bangun datar yang dibatasi oleh tiga buah sisi dam memiliki tiga titik sudut.
segitiga umum
Dimana jumlah ketiga titik sudut tersebut adalah 180 derajat yang ditemukan oleh Matematikawan Euclid. Hal ini memungkinkan untuk kita menghitung salah satu dusut jika keduanya diketahui.
Berdasarkan panjang sisinya, segitiga dapat diklasifikasikan menjadi 3 yaitu :
  1. Segitiga sama sisi, yaitu segitiga yang ketiga sisinya sama panjang, maka masing-masing sudutnya sama besar yaitu 60 derajat.
  2. Segitiga sama kaki, yaitu segitiga yang dua dari tiga sisinya sama panjang, maka dua sudut dari tiga sudutnya sama besar.
  3. Segitiga sembarang, yaitu segitiga yang ketiga sisinya memiliki panjang yang berbeda, sehingga besar setiap sudutnya berbeda.
232422
Segitiga sama sisiSegitiga sama kakiSegitiga sembarang
Menurut besar sudut terbesarnya, segitiga dapat dibagi menjadi tiga yaitu :
  1. Segitiga siku-siku merupakan segitiga yang salah satu besar sudutnya 90ยบ . Sisi yang berada didepan sudut 90ยบ disebut hipotenusa atau sisi miring.
  2. Segitiga lancip merupakan segitiga yang besar semua sudutnya < 90ยบ.
  3. Segitiga tumpul merupakan segitiga yang besar salah satu sudutnya >90ยบ.
252627
Segitiga siku-sikuSegitiga tumpulSegitiga lancip
Rumus untuk menghitung luas segitiga yaitu
L = ½.alas.tinggi
Sedangkan rumus keliling lingkaran yaitu :
K = sisi1 + sisi2 + sisi3
Teorema Heron
Teorema ini biasanya digunakan untuk mencari luas segitiga sembarang, misal a, b dan c adalah sisi-sisinya maka
  • 28
dimana
  • 34

Dalam kasus segitiga sama sisi yang bersisikan a maka untuk mencari luas dan kelilingnya dapat juga menggunakan rumus sebagai berikut :
  • 29
  • 30

Dalil Phytagoras
Dalil ini hanya berlaku untuk segitiga siku – siku.
31
Phytagoras menyatakan bahwa c²=a²+b²
Jika terdapat tiga buah bilangan yang memenuhi pernyataan diatas maka ketiga bilangan tersebut disebut triple phytagoras.
Triple phytagoras dapat dibangun dengan menggunakan rumus diatas dengan memasukan sebuah nilai n diman n adalah bilangan bulat positif.

Lingkaran dalam dan luar segitiga
Lingkaran dalam segitiga merupakan suatu lingkaran yang berada didalam segitiga serta menyinggung ketiga sisi segitiga, dimana jari-jarinya dapat dicari dengan menggunakan rumus sebagai berikut
32
dimana :
r = jari-jari lingkaran dalamsegitiga
L= luas segitiga
s= setengah keliling segitiga
Lingkaran luar segitiga merupakan suatu lingkaran yang berada diluar segitiga dan keliling lingkaran tersebut menyinggung perpotongan tiga garis segitiga ( titik sudut ). Jari-jari lingkaran luar segitiga dapat dicari menggunakan rumus sebagai berikut
33
dimana :
R = jari-jari lingkatan luar segitiga
a,b,c = sisi segitiga
L = luas segitiga
Demikian Rumus Mencari Luas Segitiga Lengkap telah selesai dipaparkan, semoga bermanfaat. Rumus untuk bangun datar yang lain dapat anda lihat pada artikel sebelumnya seperti pada Rumus Persegi Panjang.

cara menghitung luas segitiga jika diketahui panjang ketiga sisi-sisinya.

Rumus Heron atau formula Heron diambil dari nama ahli matematika Yunani yang bernama Heron dari Alexandria. Rumus Heron terdapat di dalam buku yang ditulis oleh Heron yang berjudul “Metrica” sekitar tahun 60 Masehi. Buku tersebut berisi kumpulan pengetahuan tentang matematika pada masa tersebut. Dalam buku tersebut Heron menuliskan hubungan antara luas segitiga dengan panjang ketiga sisinya.

Rumus Heron
Rumus Heron sering disebut juga dengan formula Heron atau Teorema Heron. Rumus Heron menyatakan bahwa sebuah luas sebuah segitiga sembarang dapat dihitung secara langsung jika diketahui panjang masing-masing sisi segitiga tersebut. Menghitung luas segitiga dengan menggunakan rumus Heron jauh lebih sederhana dan lebih mudah dibandingkan dengan menggunakan pendekatan trigonometri. Dalam persamaan matematika rumus Heron dapat dijelaskan sebagai berikut.

Cara menghitung luas segitiga dengan rumus Heron

Cara Menghitung Luas Lingkaran Mengunakan Rumus Heron
Untuk menghitung luas segitiga sembarang dengan panjang sisi-sisi a, b, dan c menggunakan rumus Heron digunakan dua tahapan berikut.
1. Hitung semiperimeter (setengah keliling) segitiga dengan menggunakan rumus ½ (a+b+c).
2. Hitung luas segitiga dengan rumus Luas = akar kuadrat dari s(s-a)(s-b)(s-c).

Contoh Cara Menghitung Luas Segitiga dengan Rumus Heron
1. Soal: Diketahui sekeping keramik dipotong berbentuk segitiga sembarang dengan panjang sisi-sisi  10 cm, 13, dan 17 cm. Berapa luas permukaan keramik tersebut? (Petunjuk: Setengah keliling s = ½ (a+b+c), Luas =  akar kuadrat dari (s(s-a)(s-b)(s-c)). Jawab: Setengah keliling s = ½ (10+13+17) = ½ (40) = 20 cm. Luas permukaan keramik = akar kuadrat dari (20(20-10)(20-13)(20-17)) = akar kuadrat dari (20(10)(7)(3)) =akar kuadarat dari (4200) = 64,807 cm2.
2. Soal: Selembar kertas berbentuk segitiga sama sisi memiliki panjang sisi-sisi 6 inch. Berapa luas permukaan kertas tersebut? (Petunjuk: Setengah keliling s = ½ (a+b+c), Luas =  akar kuadrat dari (s(s-a)(s-b)(s-c)). Jawab: Setengah keliling s = ½ (6+6+6) = ½ (18) = 9 inch. Luas permukaan kertas = akar kuadrat dari (9(9-6)(9-6)(9-6)) = akar kuadrat dari (9(3)(3)(3)) =akar kuadarat dari (243) = 15,588 inch2.
3. Soal: sepotong kaca berbentuk sebuah segitiga siku-siku dengan panjang sisi siku 12 cm dan 16 cm. Sisi alasnya adalah 16 cm dan sisi tingginya 12 cm. Panjang sisi miringnya 20 cm. Hitung luas segitiga tersebut dengan menggunakan rumus setengah alas kali tinggi dan dengan menggunakan rumus Heron. (Petunjuk: Setengah keliling s = ½ (a+b+c), Luas =  akar kuadrat dari (s(s-a)(s-b)(s-c)). Jawab: Luas segitiga menurut rumus setengah alas kali tinggi = ½ (16) (12) = 96 cm2. Setengah keliling s = ½ (12+16+20) = 24. Luas segitiga menurut rumus Heron = akar kuadrat dari (24 (24-12) (24-16) (24-20)) = akar kuardat dari (24 (12) (8) (4)) akar kuadrat dari (9216) = 96 cm2.

CARA MENGHITUNG LUAS SEGITIGA DENGAN MENGGUNAKAN PROGRAM KOMPUTER dengan Pascal

program luas;
uses crt;

var

a,t: integer;

L: real;
begin
clrscr;
write(‘Masukan Nilai Alas:’);
readln (a);
write(‘Masukan Nilai Tingi:’);
readln(t);
writeln(‘ ‘);
L:=(a*t)/2;
writeln(‘Luas Segitiga adalah =’,L:6:2);
readln;
end.

hasilnya seperti dibawah ini:
Masukan Nilai Alas:12

Masukan Nilai Tingi:8

Luas Segitiga adalah = 48.00
MENGHITUNG LUAS SEGITIGA DENGAN MENGGUNAKAN FLOWCHART

Input    : panjang dan lebar
Proses  : panjang x lebar
Output : luas persegi panjang

Algoritma    : 1. Masukkan panjang
                      2. Masukkan lebar
                      3. Luas Persegi panjang adalah panjang dikalikan lebar
                      4. Tampilkan luas persegi panjang

Pseudocode : Input panjang
                       Input lebar
                       Luas = panjang x lebar
                       Print luas




CARA MENGHITUNG LUAS SEGITIGA DENGAN MENGGUNAKAN BLOG/WEB
PHP dapat menghitung apapun seperti matematika.Dan Berikut Tips dan trik yang saya buat untuk anda



Persiapan


1) Notepad (Notepad++ ,EditPlus dll)
1) XAMPP Control Panel


Langkah-langkah
    
    Pastikan kalian sudah membuka notepad anda,kemudian :

1) Buat file atau copy code di bawah ini,kemudian save dengan nama segitiga.php

 <html>
<head>
<title>.:: Menghitung Luas Segi Tiga::.</title>
</head>
<body>
<style>
table {
 background-color:blue;
 box-shadow: 0px 30px 50px #000;
 }
td {
 font-family:cursive;
 font-size:20px;
 color:#fff;
 font-weight:bolder;
}

input {
 font-family:impact;
 font-size:20px;
 color:#fff;
 background-color:#000;
 }
</style>
<font face=cursive>
<center><h3><u>Menghitung Luas Segitiga</u></h3></center>
<form action="proses.php" method="get">
<table align=center cellspacing=40>
<tr>
<td>Alas</td>
<td>:</td>
<td><input type=text name=alas size=20></td>
</tr>
<tr>
<td>Tinggi</td>
<td>:</td>
<td><input type=text name=tinggi size=20></td>
</tr>
<tr>
<td colspan=3 align=center><input type=submit value=hasil></td>
</tr>
</table>
</form>
</body>
</html>

2) Kemudian Buat lagi file atau copy code,lalu save dengan nama proses.php

 <html>
<body>
<font><h3><u>Luas Segitiga</u></h3>
</center>

<style>
table {
 background-color:blue;
 box-shadow: 0px 30px 50px #000;
 }

td {
 font-family:cursive;
 font-size:20px;
 color:#fff;
 font-weight:bolder;
}

input {
 font-family:impact;
 font-size:20px;
 color:#fff;
 background-color:#000;
 }
</style><form action="segitiga.php" method=get>
<?
    $a=$_GET['alas'];
$b=$_GET['tinggi'];
$luas=0.5*$a*$b;
echo "<table align=center cellpadding=30>";
echo "<tr>";
echo "<td>Alas</td>";
echo "<td>:</td>";
echo "<td> {$_GET ['alas']} </td>";
echo "</tr>";
echo "<tr>";
echo "<td>Tinggi</td>";
echo "<td>:</td>";
echo "<td> {$_GET ['tinggi']} </td>";
echo "</tr>";
echo "<tr>";
echo "<td>Luas Segitiga</td>";
echo "<td>=</td>";
echo "<td>$luas</td>";
echo "</tr>";
echo "<tr>";
echo "<td colspan=3 align=center><input type=submit value=ulang></td>";
echo "</tr>";
echo "</table>";
?>
</form>
</body>
</html>

Categories:
Pin It

Related Post:



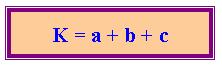
0 komentar :

Post a Comment

Silahkan Berkomentar Sesuai Dengan Topik, Jangan Menggunakan Kata-Kata Kasar, Komentar Dengan Link Aktif Tidak Akan Dipublikasikan

ttd

Admin Blog