Home » matematika » solusi persamaan diferensial parsial

solusi persamaan diferensial parsial

PERSAMAAN DIFRENSIAL PARSIAL

Persamaan diferensial parsial (PDP) merupakan  persamaan yang di dalamnya terdapat suku-suku diferensial parsial, yang dalam matematika diartikan sebagai suatu hubungan yang mengaitkan suatu fungsi yang tidak diketahui, yang merupakan fungsi dari beberapa variabel bebas, dengan turunan-turunannya melalui variabel-variabel yang dimaksud.

PDP digunakan untuk melakukan formulasi dan menyelesaikan permasalahan yang melibatkan fungsi-fungsi yang tidak diketahui, yang merupakan dibentuk oleh beberapa variabel, seperti penjalaran suara dan panas, elektrostatika, elektrodinamika, aliran fluida, elastisitas, atau lebih umum segala macam proses yang terdistribusi dalam ruang, atau terdistribusi dalam ruang dan waktu. Kadang beberapa permasalahan fisis yang amat berbeda memiliki formulasi matematika yang mirip satu sama lain.

BENTUK PERSAMAAN DIFRENSIAL PARSIAL

Bentuk paling sederhana dari persamaan diferensial adalah

\frac{\part u}{\part x}=0\,
di mana u suatu fungsi tak diketahui dari x dan y. Hubungan ini mengisyaratkan bahwa nilai-nilai u(x,y) adalah tidak bergantung dari x. Oleh karena itu solusi umum dari persamaan ini adalah

u(x,y) = f(y),\,
di mana f adalah suatu fungsi sembarang dari variabel y. Analogi dari persamaan diferensial biasa untuk persamaan ini adalah

\frac{du}{dx}=0\,
yang memiliki solusi

u(x) = c,\,
di mana c bernilai konstan (tidak bergantung dari nilai x). Kedua contoh di atas menggambarkan bahwa solusi umum dari persamaan diferensial biasa melibatkan suatu kostanta sembarang, akan tetapi solusi dari persamaan diferensial parsial melibatkan suatu fungsi sembarang. Sebuah solusi dari persamaan diferensial parsial secara umum tidak unik; kondisi tambahan harus disertakan lebih lanjut pada syarat batas dari daerah di mana solusi didefinisikan. Sebagai gambaran dalam contoh sederhana di atas, fungsi \!f(y) dapat ditentukan jika \!u dispesifikasikan pada sebuah garis \!x=0.
 
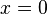I. TAFSIRAN TURUNAN PARSIAL

Andaikan, z = f (x, y) adalah suatu permukaan fungsi dua variabel dari x dan y. Bilamana y diambil konstan, misalnya y = y0. Berkas permukaan tersebut dinyatakan dengan dua persamaan yaitu :

Z = f (x,y) dan y= y0

Berkas lengkungan permukaan tersebut merupakan perpotongan permukaanz = f (x,y) dan bidang y= yo . Jadi turunan parsial f terhadap x, fx (x,y) di (x0,y0) dapat ditafsirkan sebagai gradian garis singgung kurva yang diberikan oleh z = f (x,y) dan y=y0 dititik (x0,y0), f (x0,y0 ) dengan zo =f (x0,y0).

Dengan pendekatan yang sama, turunan parsial f terhadap y, fy(x,y) ditafsirkan merupakan gradiean garis singgung kurva pada permukaan, z = f (x,y) dan x=x0 dititik P0 (x0,y0,z0) pada bidang x= x0. Karena setiap turunan merupakan ukuran dari suatu laju perubahan, maka turunan parsial dapat diartikan sebagai laju perubahan. Sehingga fx (x,y) dapat diartikan sebagai laju perubahan dari f (x,y) terhadap x bilamana y konstan. Demikian sebaliknya untuk fy(x,y).

II. TURUNAN PARSIAL FUNGSI DAN VARIABEL

Andaikan diberikan fungsi n variabel dari x1,x2,x3,.......xn dengan persamaan :

W=f (x1,x2,x3,.......xn)

III. TURUNAN PARSIAL ORDE TINGGI

Pada umumnya parsial fungsi dua variabel dari x dan y yakny fx(x,y) dan fy (x,y) masih memuat variabel x dan y. Fungsi turunan parsialfx(x,y) dan fy (x,y) masih dapat diturunkan terhadap x dan y, hasinya disebut turunan parsial orde 2.

PENERAPAN DIFERENSIAL PARSIAL DENGAN SAINS

Diferensial parsial digunakan dalam penerapan sains dalam menghitung laju perubahan tekanan, volume dan suhu pada hukum gas ideal.
Categories:
Pin It

Related Post:



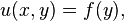
0 komentar :

Post a Comment

Silahkan Berkomentar Sesuai Dengan Topik, Jangan Menggunakan Kata-Kata Kasar, Komentar Dengan Link Aktif Tidak Akan Dipublikasikan

ttd

Admin Blog